计算机网络网络安全

网络安全吗？答案是否定的，网络可以认为是十分不安全的。

网络安全是指网络系统的硬件、软件及其系统中的数据受到保护，不因偶然的或者恶意的原因而遭受到破坏、
更改、泄漏，系统连续可靠正常地运行，网络服务不中断。

网络安全基本属性

机密性 confidentiality

只有发送方与预定接收方能够理解报文内容

发送方加密报文
接收方解密报文

身份认证 authentication

发送方与接收方希望确认彼此的真实身份

信息完整性 message integrity

发送方与接收方希望确保信息未被篡改（传输途中或者后期），发生篡改一定会被检测到

可访问与可用性 access and availability

网络服务必须对被授权的用户可访问与可用

网络安全基本特征

相对性

只有相对安全，没有绝对安全

时效性

新的漏洞与攻击方法不断发现，某个时期相对安全

不确定性

攻击时间、攻击者、攻击目标和攻击发起的地点都具有不确定性

复杂性

网络安全是一项系统工程，需要技术的和非技术的手段（法律）

重要性

网络安全关乎国家、政府、企业、个人安全

网路安全研究领域

入侵者（bad guys）如何攻击计算机网络
如何防护网络对抗攻击
如何设计网络体系结果免疫（immune）攻击

Internet 最初设计几乎没有考虑安全性，最初愿景：一组彼此信任的互助用户连接到一个透明网络进行信息共享。

Internet协议设计者扮演了追赶者（catch-up）角色。网路安全需要在网络各个层次考虑。

拟人模型

Alice、Bob、Trudy。

网络中的 Bob Alice

电子交易过程的 Web 浏览器/服务器
网络银行的客户端/服务器
DNS 服务器
路由器之间交换路由表更新

网络中的 Trudy

通过 Internet 向主机植入恶意软件（malware）
- 病毒（virus）
- 蠕虫（worm）
- 间谍软件（spyware）：记录键盘输入、web 站点访问、向收集站点上传信息等

被感染的主机可能加入僵尸网络（botnet），用于发送垃圾邮件、DDoS 攻击等。

网络安全威胁

窃听 eavesdrop

窃听信息

插入 insert

主动在连接中插入信息

假冒 impersonation

可以通过伪造 spoof 分组中的源地址（或者分组的任意其他字段）

劫持 hijacking

通过移除/取代发送方或者接收方接管 take over 连接

拒绝服务 Dos denail of service

阻止服务器为其他用户提供服务，向接收方恶意泛洪 flood 分组，淹没 swamp 接收方。

带宽耗尽
资源耗尽

DDoS 分布式拒绝服务攻击。反射式 DDoS 攻击。

对策：在到达主机前过滤掉泛洪分组（比如 SYN），可能好坏一起扔，误杀。追溯 traceback 攻击源。

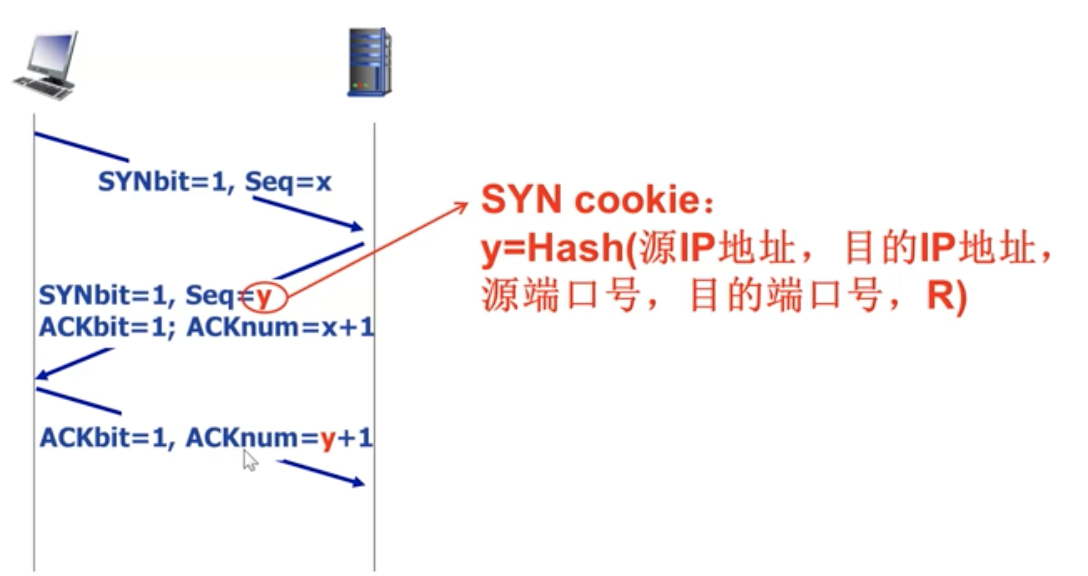
攻击者只发送第一次握手，此时服务器处于半连接状态（第二次握手），服务器就分配了资源。 SYN cookie
延缓资源分配，在收到客户端第三次握手时再分配资源，那服务器在收到第三次握手时怎么知道之前已经进行了
两次握手但未分配资源呢，答案就是服务器返回的序列号，SYN cookie：y=Hash(源 IP 地址，目的 IP 地址，源端口号，目的端口号，R（随机数）)

映射 mapping

发起攻击前：”探路”，踩点，case the joint，找出网络上运行什么服务
利用 ping 命令确定网络上主机的地址
端口扫描 port scanning 依次尝试与每个端口建立 TCP 连接
nmap 端口扫描工具

对策：countermeasures

记录到达的网络流量
分析、识别出可疑活动（IP地址和端口依次扫描）

分组嗅探 sniffing

必须是广播介质，共享式以太网、无线网络等，混杂模式 promiscuous 网络接口可以接收/记录所有经过的分组/帧，可以读到所有未加密数据。比如 wireshark 工具。

对策：组织中的所有主机都运行软件，周期性检测网络接口是否工作在混杂模式。或者每段广播介质连接一台主机（如交换式以太网）。

IP 欺骗 spoofing

直接由应用生成原始 IP 分组，可以设置分组的源 IP 地址字段为任意值。（原始套接字 raw socket）。接收方无法判断源地址是否被欺骗。

对策：入口过滤 ingress filtering，路由器不转发源 IP 地址无效的 IP 分组比如源 IP 地址不属于所连接网络，很有效，但是不能强制所有网络都执行入口过滤。

密码学

密码学 cryptography 术语

对称密钥加密：Bob 和 Alice 共享相同（对称）密钥（密钥如何分发）
公开密钥加密：Alice 利用 Bob 的公钥加密，一旦加密后 Alice 就无法解开了，只能由 Bob 的密钥解开。

破解加密方法

唯密文攻击

cipher-text only attack：入侵者只截获密文，基于对密文饿的分析进行破解

两条途径：

暴力破解 brute force，尝试所有可能的密钥
统计分析

已知明文攻击

known-plaintext attack，入侵者已知（部分）明文以及与之匹配的密文。

选择明文攻击

chosen-plaintext attack，入侵者可以获取针对选择的明文的密文。

传统加密算法

替代密码 substitution

利用一种东西替代另一种东西

凯撒密码 casesar cipher

一个字母替代另一个字母，将一个字母利用字母表中该字母后面的第k个字母替代，此时 k 就是密钥

单码/字母替代密码 monoalphabetic cipher

一个字母替代成其他字母，此时这种映射关系就是密钥

多码/字母替代加密 polyalphabetic encryption

使用多个单码替代密码，明文中不同位置的字母使用不同的单码替代密码

加密密钥为（C1=5，C2=19），C1，C2，C2，…，比如第一个位置用C1替代，第二个用C2替代，以此类推。

换位密码 transpositions

重新排列明文中的字母

置换法 permutation method

将明文划分为固定长度（d）的组，每个组内的字母按置换规则（f）变换位置，此时长度d和变换规则f就是密钥。

比如密钥为：d=4，f=（1->3, 2->1, 3->4, 4->2）。

列置换加密

将明文按行组成一个矩阵，然后按给定列顺序输出得到密文。

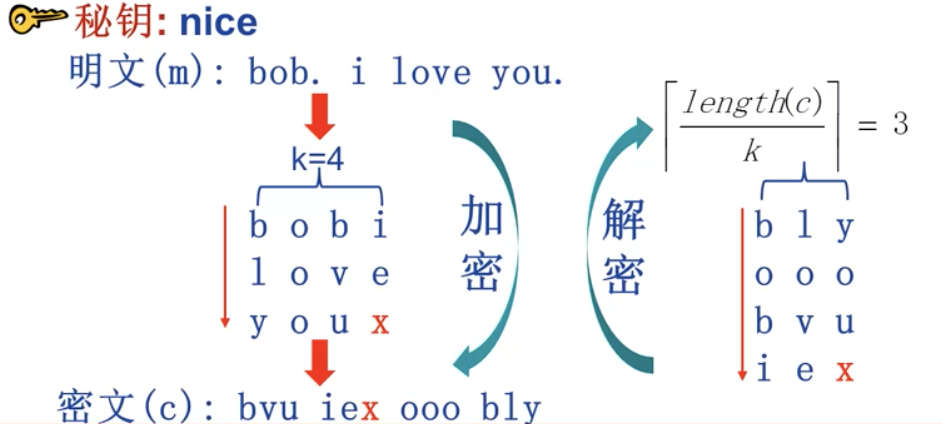
比如密钥为：k=4（矩阵的列数）（2, 3, 1, 4）输出顺序，不足用 x 替代。

可以用一个单词来表示密钥，单词长度表示列数，单词中的字母顺序表示输出顺序，单词不能出现重复。

现代加密技术

现代加密技术的基本操作包括经典的替代和置换，不在针对一个个字母，而是针对二进制位操作。

现代加密技术主要分为：

对称密钥加密
- 流密码 stream ciphers
- 分组密码，也称块密码 block ciphers
非对称密钥加密（公开密钥加密）

流密码

基本思想：首先利用密钥 K 产生一个密钥流（字节流或者比特流都可以）：Z=Z0Z1Z2…，然后使用如下规则对明文串x=x0x1x2…加密
y=y0y1y2…=Ez0(x0)Ez1(x1)Ez2(x2)，使用 Z0 对 x0 加密，一般是异或运算，解密时，使用相同的（对称加密）密钥流与密文做XOR运算。

一次性密码本属于流密码。

分组密码

将明文序列划分为长为 m 的明文组，各明文组在长为 i 的密钥组的控制下变换成长度为 n 的密文组，通常取 n=m；n>m扩展分组密码，n<m压缩分组密码。

典型分组密码结构：Feistel分组密码结构，在设计密码体制的过程中，Shannon 提出了能够破坏对密码系统进行各种统计分析攻击的两个基本操作：扩散（diffision）和混淆（confusion）。

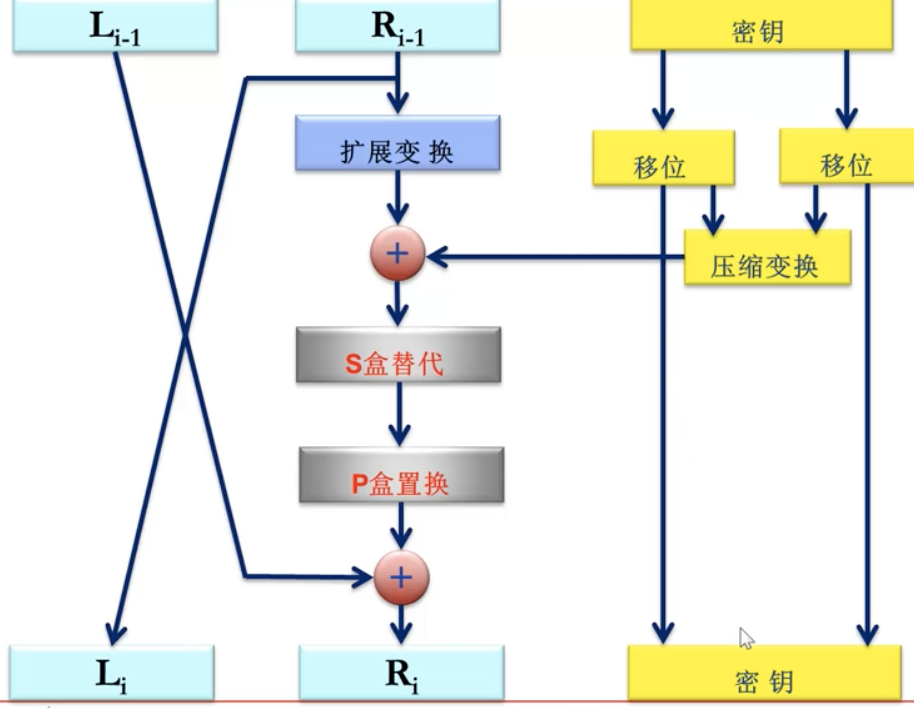
Feistel 分组密码结构

基于扩散和混淆的思考，Feistel提出通过替代和置换交替操作方式构造密码，Feistel 是一种设计原则，并非一个特殊的密码。

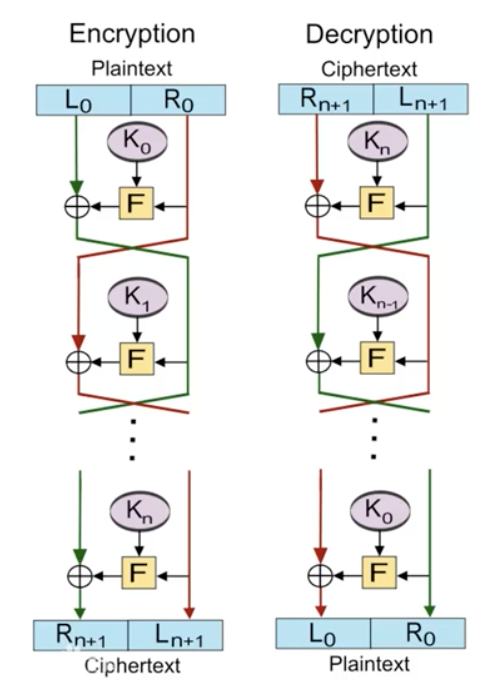
加密过程

将明文分成左右两部分，明文=（L0，R0），每一轮i=1,2,…n 计算 Li=Ri-1 Ri=Li-1 XOR F（Ri-1，Ki），
其中F是轮函数，Ki是子密钥。每一轮的左半部用上一轮的右半部替换，右半部用上一轮的左半部异或上一轮的右半部和子密钥运算的结果，
密文=（Ln, Rn）。

解密过程

密文 =（Ln, Rn），每一轮i=n,n-1,…1，计算Ri-1=Li，Li-1=Ri XOR F（Ri-1, Ki）,
其中F是轮函数，ki是子密钥，密文=（L0，R0）。

安全性

Feistel 结构的分组密码安全性取决于

分组长度，分组长度越大，安全性越高，加密速度越慢，效率越低，目前常用的分组加密算法的分组长度取64位
子密钥大小，子密钥长度增加，安全性提高，加密速度降低，设计分组密码时需要在安全性和加密效率之间进行平衡
循环次数，循环越多，安全性越高，加密效率越低
子密钥产生算法，在初始密钥给定的情况下，产生子密钥的算法越复杂，安全性越高
轮函数，一般情况下，论函数越复杂，加密算法的安全性越高

DES

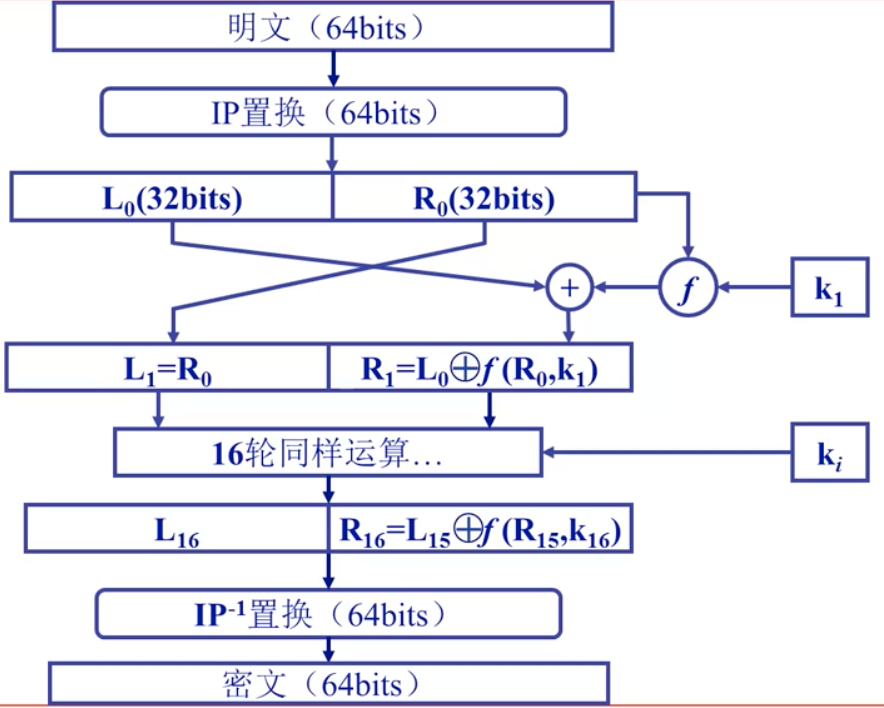
数据加密标准，Data Encryption Standard，IBM 研制的对称密钥加密。

DES 是 16 轮的 Feistel 结构密码
DES 是一个包含 16 个阶段的替代-置换的分组加密算法
DES 的分组长度是 64 位
- 64 位的分组明文序列作为加密算法的输入，经过 16 轮加密得到 64 位的秘文序列
DES 使用 56 位的密钥
DES 的每一轮使用 48 位的子密钥
- 每个子密钥是 56 位密钥的子集构成

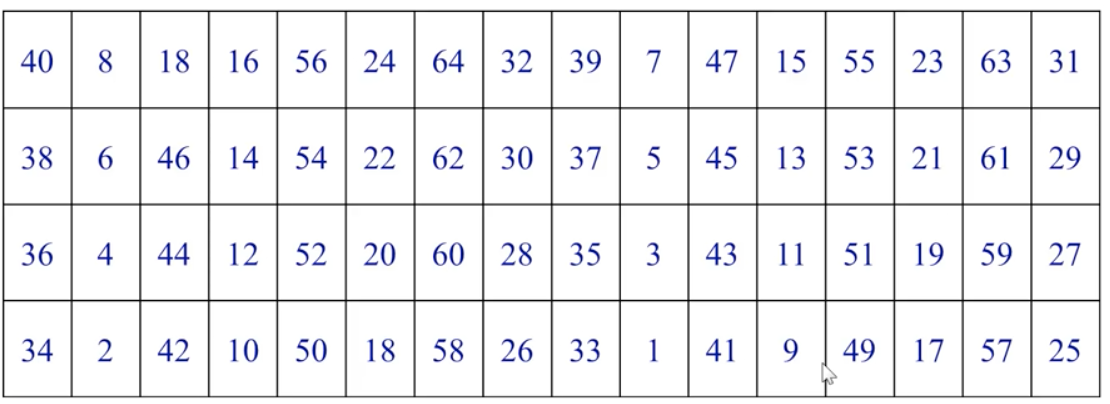
初始置换IP Initial Permutation

把输入的 64 位数据的排列顺序打乱，每位数据按照如下规则重新组合。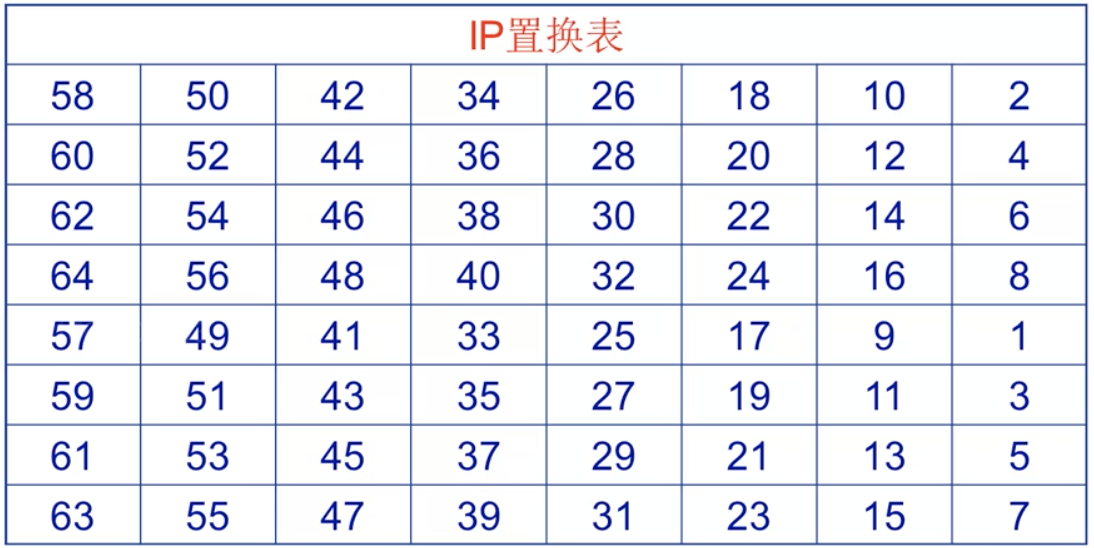

表中的每个格子都是一位数据，第一位利用第五十八位替换，一次类推。

一轮 DES

f 函数结构

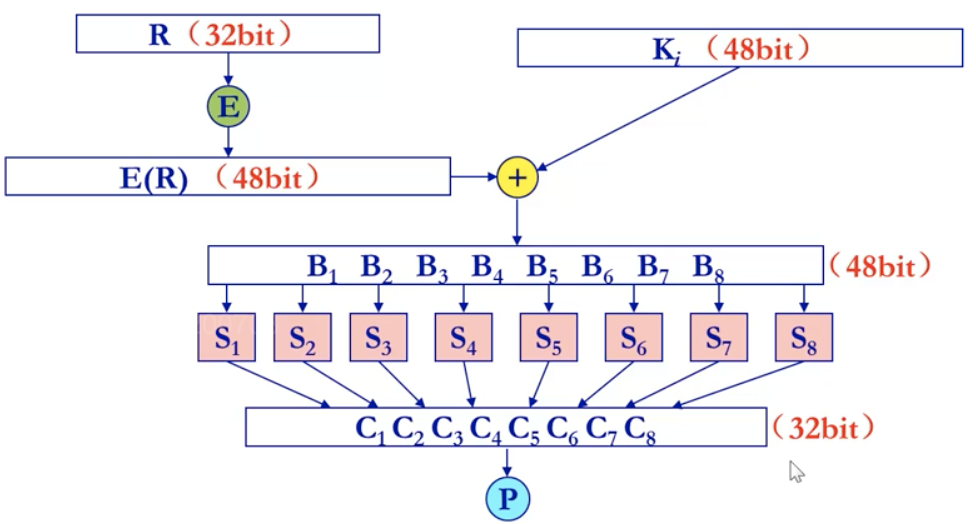
黑盒变换
多个函数/操作（E、异或、S、P）的组合函数
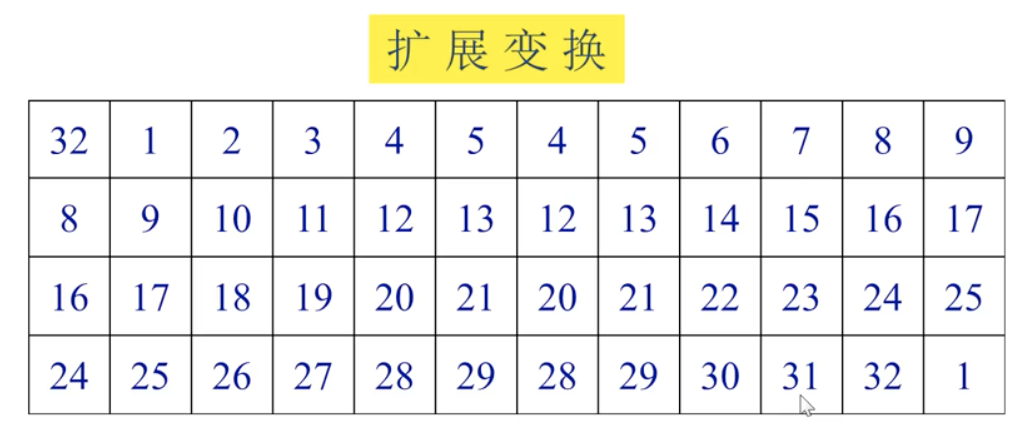
扩展变换：Expansion Permutation，也被称为E-盒，将 64 位输入序列的右半部分从 32 位扩展到 48 位
- 确保最终的密文与所有的明文位都有关

S-盒替代 s-boxes substitution

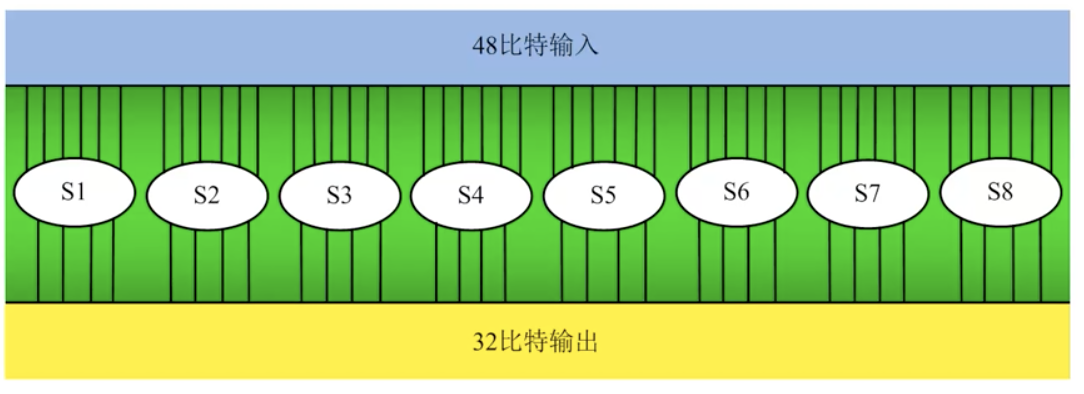
P-盒置换 p-boxes permutation

逆初始置换 Inverse Initial Permutation

初始置换和对应的逆初始置换操作并不会增强 DES 算法的安全性，主要目的是为了更容易地将明文和密文数据以字节大小放入 DES 芯片中。

每轮子密钥的生成

64 位的密钥，每个字节的第八位作为校验位。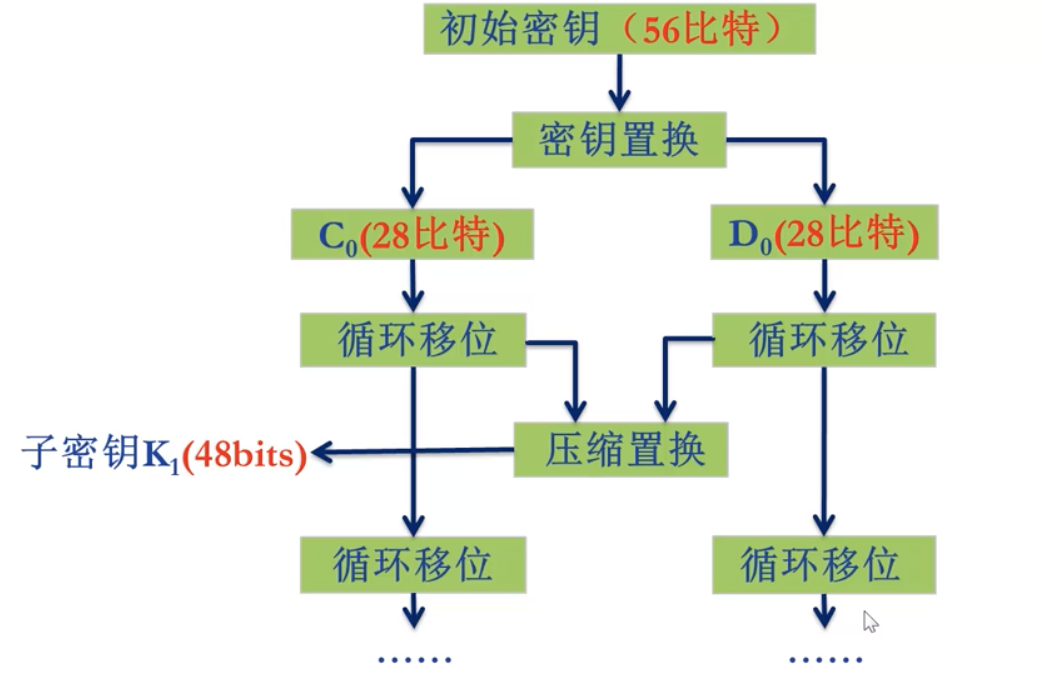

DES 的安全性

DES的 56 位密钥可能太小
- 1998年7月，EFE 电子前哨基金会宣布攻破了 DES 算法，他们使用的是不到25万美元的特殊的 DES 破译机，这种攻击只需要不到三天的时间
DES 的迭代次数可能太少
- 16次恰巧能抵抗差分分析
S 盒中可能有不安全因素
DES 的一些关键部分不应该保密（加密方法应公开，密钥需要保密）
DES 存在弱密钥和半弱密钥（移位后子密钥相同，16 轮子密钥相同或交替出现）
针对 DES 的攻击方法
- 差分分析方法 Difference Analysis Method
- 线性分析方法 Linear Analysis Method
- 旁路攻击方法 Side-Channel Attack （观察芯片耗能等）

DES 的改进

密码分组链接 CBC-cipher block chaining

算法解决了相同的明文分组加密后的数据相同问题，避免攻击者破解
加密算法的输入是当前明文组和前一次密文分组的异或
重复的明文分组不会在密文中暴露出重复关系

多重 DES

DES 密钥过短 56 bits 改成多重 DES 加密
3DES 使用 3 个密钥，执行 3 次 DES 算法
- 加密-解密-加密（EDE）使用三个密钥先加密在解密在加密
为了避免 3DES 使用 3 个密钥进行三阶段加密带来的密钥过长缺点（168bit），Tuchman 提出使用两个密钥的三重加密方法，这个方法只要求 112bit 密钥，即令 k1=k3
3DES 的第二阶段的解密并没有密码编码学上的意义，唯一优点是可以使用 3DES 解密原来的单次 DES 加密的数据

AES 高级加密标准

Advanced Encryption Standard
NIST（美国国家标准技术研究所）对称密钥加密标准，取代 DES （2001年12月）
1997年 NIST 宣布征集 AES 算法，要求
- 可公开加密方法
- 分组加密。分组长度为 128 位
- 至少像 3DES 一样安全
- 更加高效、快
- 可提供 128/192/256 位密钥
比利时学者 Joan Daemen 和 Vincent Rijmen 提出的 Rijndael 加密算法最终被选为 AES 算法

简介

不属于 Feistel 结构
加密、解密相似但不完全对称
支持 128/192/256 数据块大小
支持 128/192/256 密钥长度
有较好的数学理论作为基础
结构简单、速度快
算法特点
- 分组长度和密钥长度均可变 128/192/256bit
- 循环次数允许在一定范围内根据安全要求进行修正
- 汇聚了安全、效率、易用、灵活等优点
- 抗线性攻击和抗差分攻击的能力大大增强
- 如果 1 秒暴力破解 DES，则需要 149 万亿年破解 AES

公钥密码学

对称密钥加密需要发送方与接收方知道共享的秘密密钥，最初如何商定密钥？

公开密钥加密

完全不同的方法 Diffie-Hellman76 RSA78
发送方与接收方无需共享秘密密钥
公开密钥（公钥）完全公开
私有密钥（私钥）只有接收方知道

要求

公钥加密和私钥解密需要能还原数据
给定公钥不可能计算得到私钥

RSA

Rivest、Shamir、Adelson algorithm

RSA 预备知识

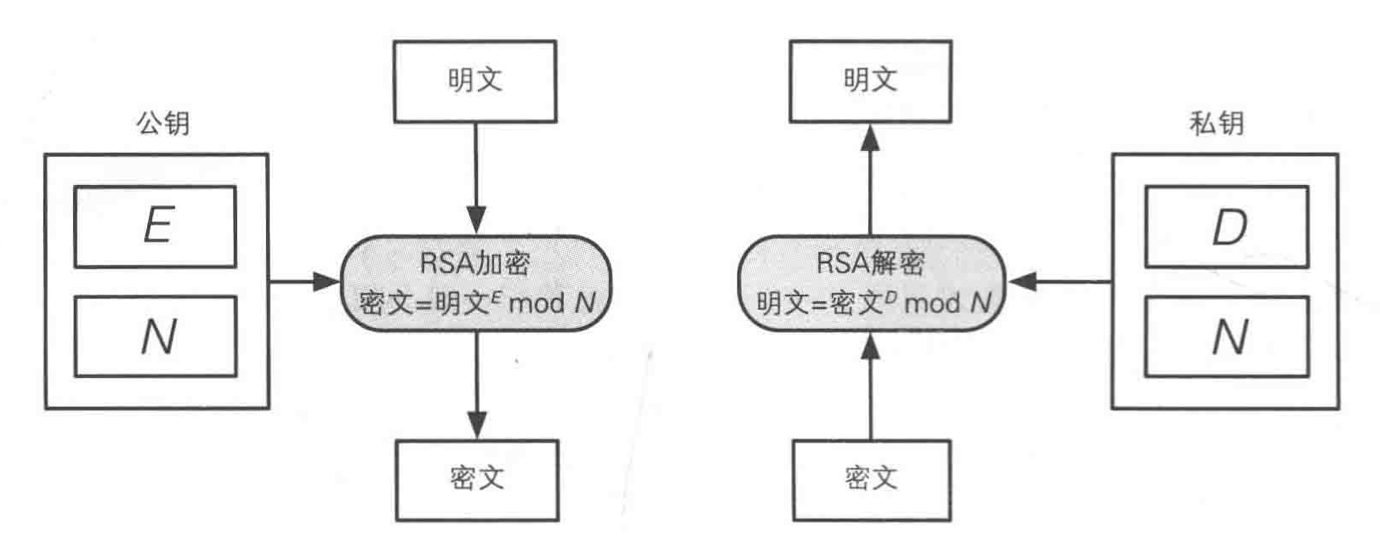
报文/信息（message）仅仅是一个比特模式 bit pattern
每个比特模式可以表示为一个唯一的整数
因此，加密一个报文就等价于加密一个数
比如 m = 10010001，可以唯一的表示为十进制数145，为了加密 m，我们可以加密对应的数（145），得到一个新的数（密文）。

RSA 生成公钥/私钥对

选择两个大质数 p 和 q （如 1024 bits 的大质数）
计算 n= pq，z=(p-1)(q-1)
选择 e （满足 e < n），使 e 与 z 之间没有公因子，即 e，z互质(relatively prime)
选择 d 使 ed - 1 刚好可以被 z 整除（即 ed mod z = 1）
公钥 = (n, e)，私钥 = (n, d)

RSA 加密、解密

给定公钥 (n, e) 和私钥(n, d)
加密报文 m (m<n)时计算 c = m^e mod n
解密密文 c 时，计算 m = c^d mod n

RSA 另外一个重要性质

利用公钥加密，可以利用私钥解密，利用私钥加密，可以利用公钥解密。

RSA 为什么安全

RSA 的安全性建立在大数分解和素性检测这个数论难题的基础上
- 即将两个大素数相乘在计算上容易实现，而将该乘积分解的计算量相当大

RSA的实际应用

RSA 的幂运算强度很大，速度慢
DES 至少比 RSA 快 100 倍
实际应用中：
- 利用公钥加密建立安全连接，然后建立第二个密钥-对称会话密钥，用于加密数据

会话密钥 session key

Bob 与 Alice 利用 RSA 交换对称会话密钥
一旦双方确认会话密钥，则利用会话密钥加密/解密会话数据

身份认证 Authentication

AP1.0

Alice 声明 I am Alice，在网络中，Bob 看不见 Alice，因此 Trudy 可以简单的声明她就是 Alice。

AP2.0

Alice 在 IP 分组中声明 I am Alice，IP 分组包含 Alice 的源 IP 地址，Trudy 可以构造一个分组，欺骗为 Alice 的 IP 地址。

AP3.0

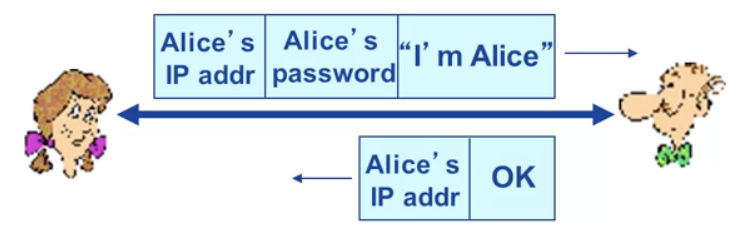
Alice 声明 I am Alice 的同时，发送她的秘密口令进行证明，Trudy 嗅探 Alice 的分组，提取口令。

AP3.1

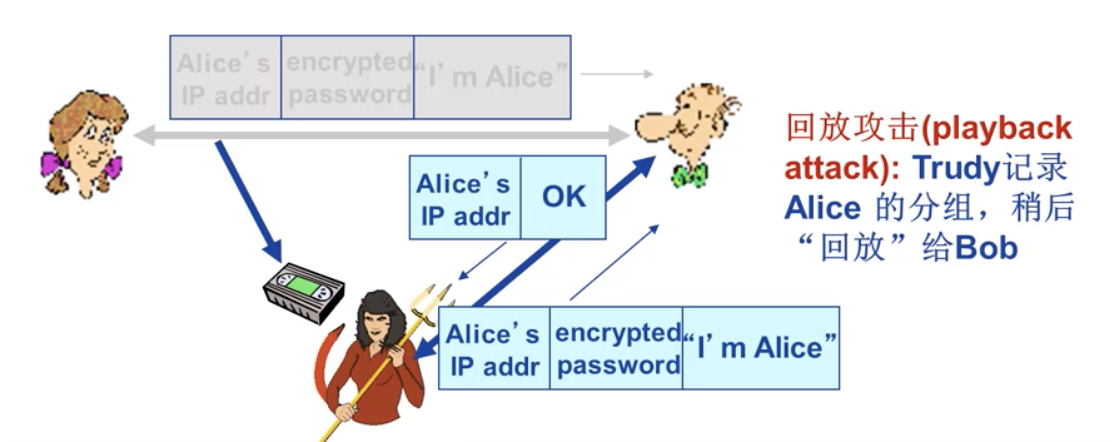
Alice 声明 I am Alice 的同时，发送她的加密的秘密口令进行证明。

回放攻击 playback attack，Trudy 记录 Alice 的分组，稍后回放给 Bob。

AP4.0

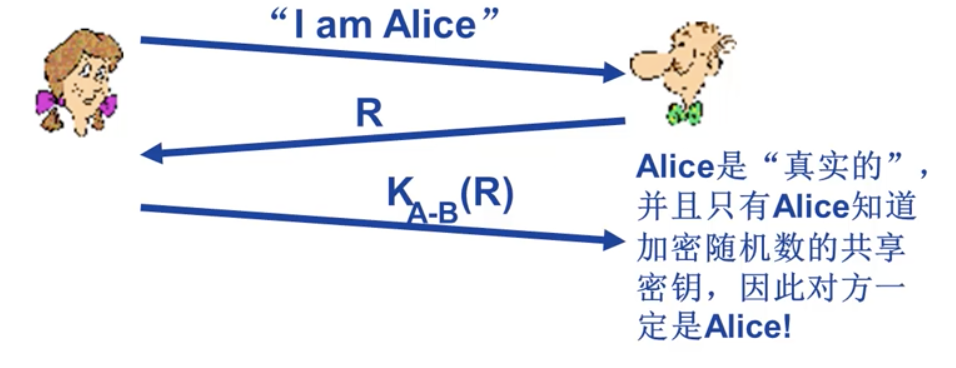
目标：避免回放攻击

一次性随机数（nonce）：一个生命期内只使用一次的数 R。

为了证明真实的 Alice，Bob 向 Alice 发送一个随机数 R，Alice 必须返回 R，并利用共享密钥进行加密。

不足之处：在发送消息之前必须共享密钥。

AP5.0

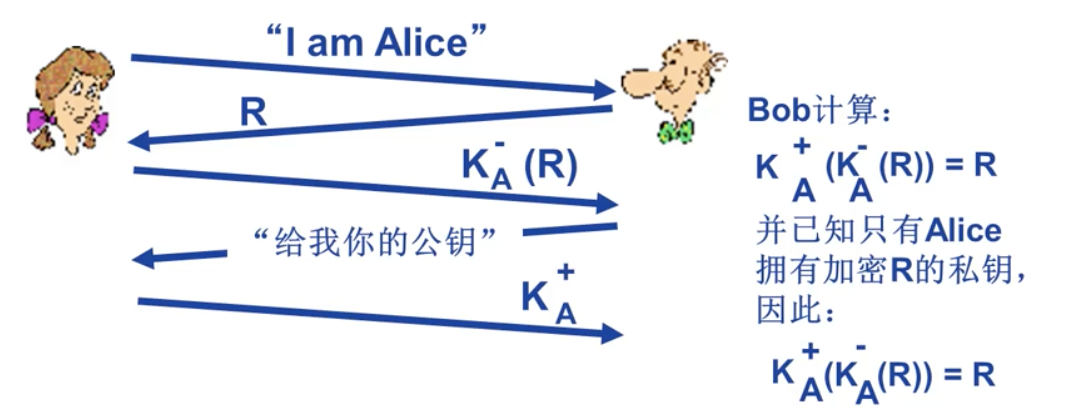
ap4.0 需要共享密钥，是否可以利用公钥技术？

ap5.0 利用一次性随机数以及公钥加密技术。

中间人攻击 man in the middle attack，Trudy 向 Bob 假扮 ALice，向 Alice 假扮 Bob。

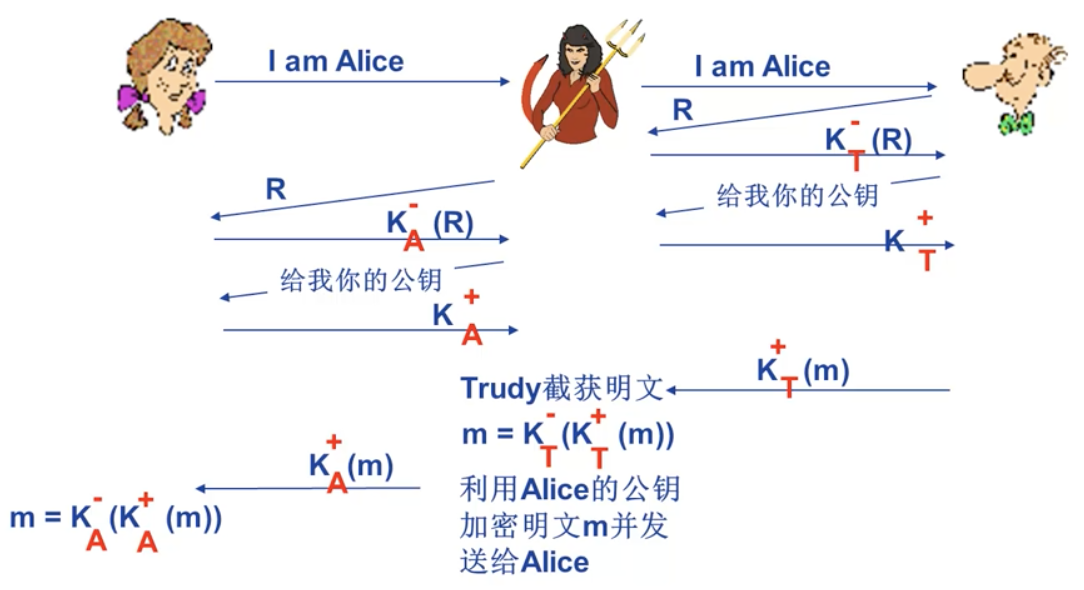
通信似乎正常进行，事实上通信所有内容都被中间人截获。

很难检测：

Bob 和 Alice 可以收到彼此发送的所有信息
问题是 Trudy 也收到了所有信息

之所以通信被攻破是因为密钥可信性问题，即密钥分发问题？

报文完整性

报文/消息完整性 message integrity，也称为报文/消息认证（或报文鉴别），目标是：

证明报文确实来自声称的发送方
验证报文在传输过程中没有被篡改
预防报文的时间、顺序被篡改
预防报文持有期被修改
预防抵赖
- 发送方否认
- 接收方否认

密码散列函数

密码散列函数 Cryptographic Hash Function H(m)

散列算法公开
H(m)能够快速计算
对任意长度报文进行多对一映射，均产生定长输出
对于任意报文无法预知其散列值
不同报文不能产生相同的散列值
单向性：无法根据散列值倒推出报文
- 对于给定散列值 h，无法计算找到满足 h=H(m) 的报文 m
抗弱碰撞性 Weak Collision Resistence WCR
- 对于给定报文 x，计算上不可能找到 y 且 y!=x，使得 H(x) = H(y)
抗强碰撞性 Strong Collision Resistence SCR
- 在计算上，不可能找到任意两个不同报文 x 和 y (x!=y)，使得 H(x) = H(y)

Internet 校验和是优秀的密码散列函数吗？
Internet 校验和 (checksum) 具备散列函数的某些属性：

多对一映射
对于任意长度报文，产生固定长度的散列值（16-bit校验和）

但是，对于给定的报文其散列值，很容易找到另一个具有相同散列值的不同报文。

散列函数算法

MD5

被广泛应用的散列函数

通过四个步骤，对任意长度的报文输入，计算输出 128 位的散列值
MD5 不是足够安全
- 1996年，Dobbertin 找到了两个不同的 512-bit 块，在 MD5 计算下产生了相同的散列值

SHA-1 Secure Hash Algorithm

另一个正在使用的散列算法

要求输入消息长度小于 2^64
散列值为 160 位
速度慢于 MD5，安全性优于 MD5

报文摘要 message digests

对报文 m 应用散列函数 H，得到一个固定长度的散列码，称为报文摘要（message digest），记为 H(m)。

报文摘要对原报文很重要，可以作为报文 m 的数字指纹 fingerprint。比如借条上按的手印。

报文认证

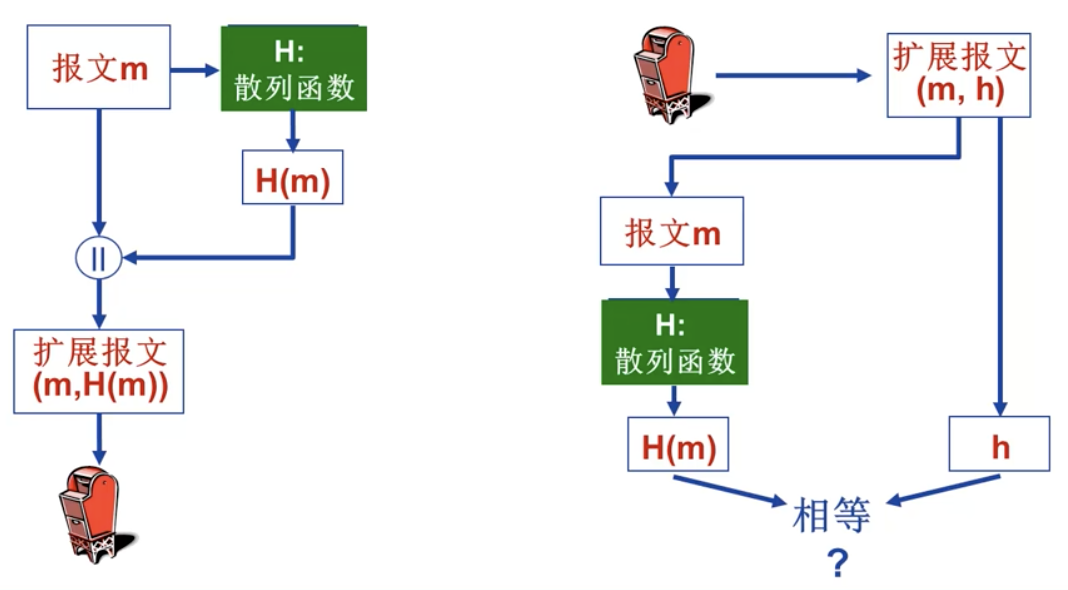
简单方案：报文+报文摘要 –> 扩展报文(m, H(m))。

这种方法仍然有缺陷，Trudy 可以用自己的报文+散列后的指纹发送给 Bob，此时 Bob 无法知道是真实的报文还是伪造后的，需要身份认证。

报文认证码 MAC Message Authentication Code

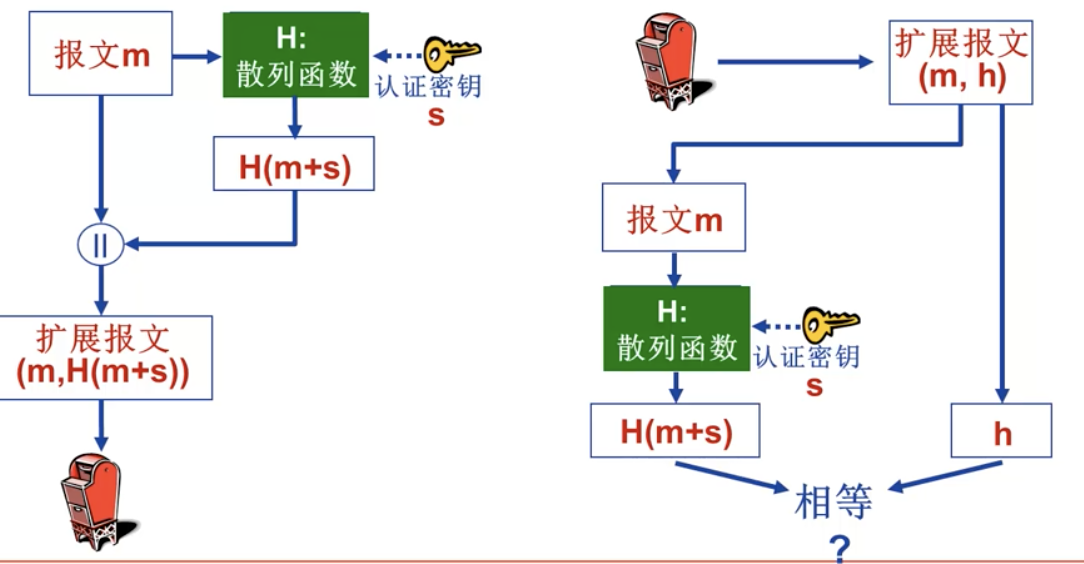
报文m + 认证密钥s + 密码散列函数 H –> 扩展报文 (m, H(m+s))

发送方和接收方共享认证密钥。

数字签名 Digital signatures

如何解决下列与报文完整性相关的问题？

否认，发送方不承认自己发生过某一报文
伪造，接收方自己伪造一份报文，并声称来自发送方
冒充，某个用户冒充另一个用户接收或发送报文
篡改，接收方收到的信息进行篡改

这些问题 MAC 很难解决。

数字签名技术是实现安全电子交易的核心技术之一。

可验证性 verifiable
不可伪造性 unforgeable
不可抵赖性 non-repudiation

怎么做呢？

对报文 m 的简单数字签名

报文加密技术是数字签名的基础，只能用公钥加密技术，不能用对称密钥加密
Bob 通过利用其私钥对 m 进行加密，创建签名报文

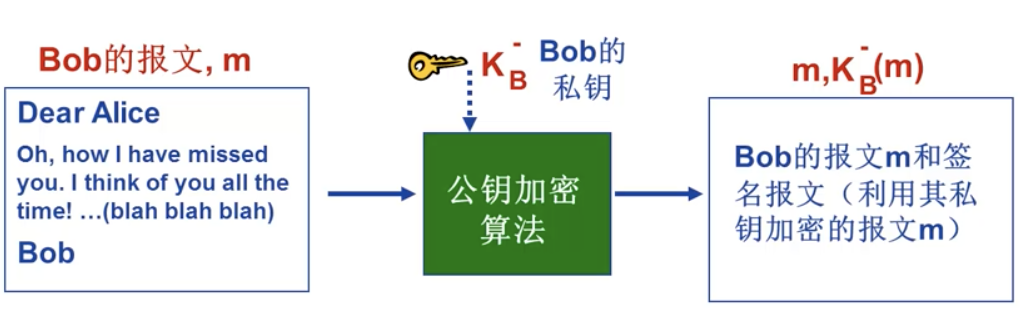
假设 Alice 收到报文 m 以及签名
Alice 利用 Bob 的公钥解密签名，并检验解密后的内容是否和收到的 m 一样来证实报文 m 是 Bob 签名的。
如果解密后的内容和 m 一致，则签名 m 的一定是 Bob 的私钥
于是 Alice 可以证实
- Bob 签名了 m
- 没有其他人签名 m 的可能
- Bob 签名的是 m 而不是其他报文 m’
不可抵赖性 non-repudiation
- Alice 可以持有 m 和签名，必要时可以提交给法院证明是 Bob 签名的m

缺点：私钥 RSA 加密慢，签名要随报文一起发送，相当于发送了两份数据。

签名报文摘要

不对原报文签名，而是签名报文摘要。

Bob 发送数字签名的报文：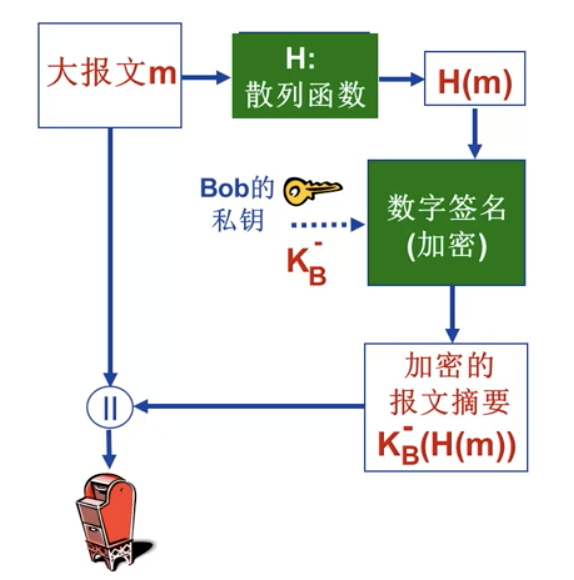

Alice 核实签名以及数字签名报文的完整性：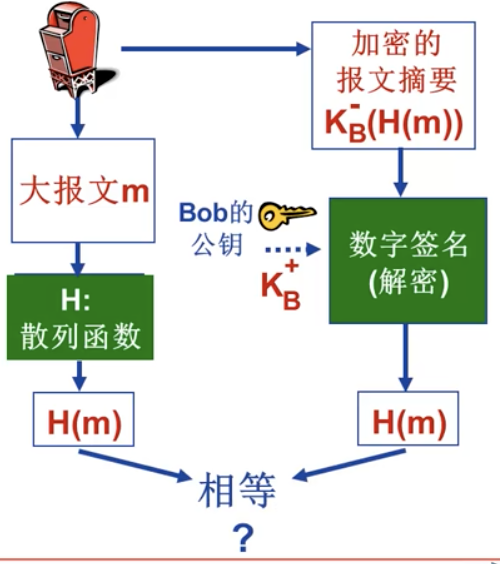

密钥分发和公钥认证中心 CA

回顾一下 AP4.0，对称密钥如何分发？两个实体在网上如何建立共享秘密密钥？

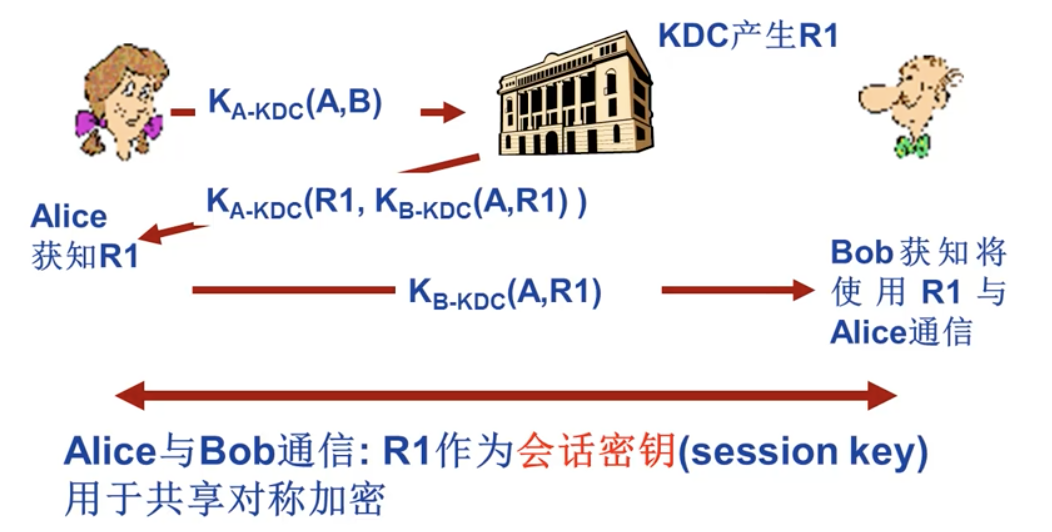
解决方案：引入可信任的密钥分发中心（Key Distribution Center-KDC）作为实体间的中介（intermediary）

（对称）密钥分发中心 KDC

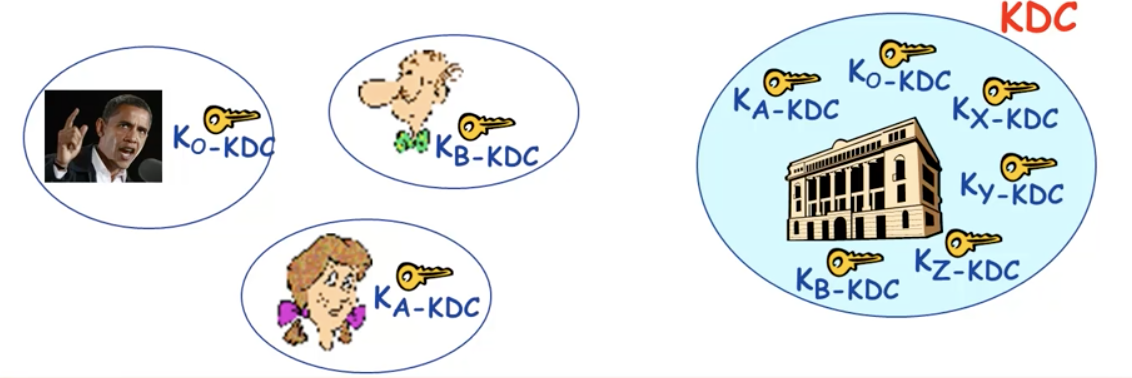
Alice 和 Bob 需要共享对称密钥
KDC：一个服务器
- 每个注册用户（很多用户）共享其与 KDC 的秘密密钥，只有用户和 KDC 知道的密钥
Alice 和 Bob 只知道自己与 KDC 之间的对称密钥，用于分别与 KD次进行秘密通信

KDC 如何支持 Bob 和 Alice 确定用于彼此通信的共享对称密钥？

（公钥）认证中心（CA）

回顾一下 AP5.0 ，中间人攻击，这些问题都是由假的公钥引起的。

比萨恶作剧

Trudy 针对 Bob 实施比萨恶作剧，Trudy 创建邮件订单，以 Bob 的名义定比萨。
Trudy 利用她的私钥签名订单，Trudy 向比萨店发送订单，Trudy 向比萨店发送她的公钥，但她声称这是 Bob 的公钥，
比萨店核实签名：然后向 Bob 递送比萨。

公钥问题：当 Alice 获得 Bob 的公钥（通过 web 网站、e-mail、磁盘等），她怎么确认这真的是 Bob 的公钥而不是 Trudy 的。

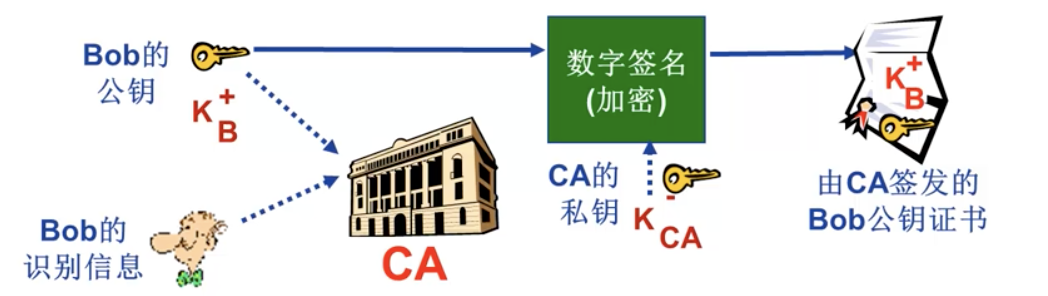
认证中心

认证中心（CA），实现特定实体 E 与其公钥的绑定
每个 E （人，路由器的等）在 CA 上注册其公钥
- E 向 CA提供身份证明
- CA 创建绑定 E 以及公钥的证书 certificate
- 证书包含由 CA 签名的 E 的公钥–CA 声明：这是 E 的公钥

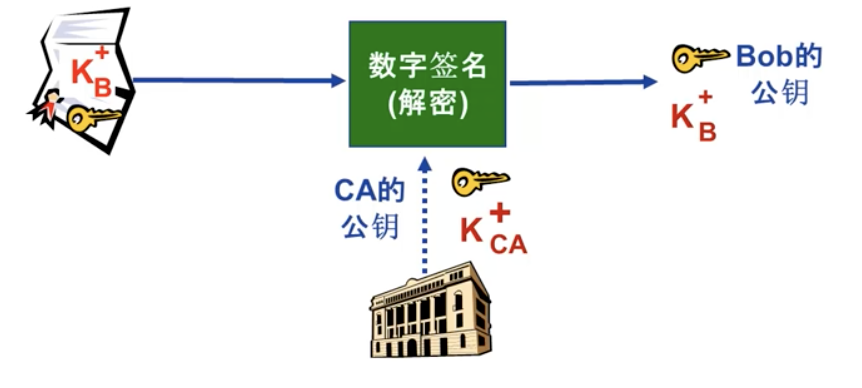
当 Alice 想要 Bob 的公钥时：

首先获取 Bob 的公钥证书（从 Bob或者其他地方）
应用 CA 的公钥（大家都知道），解密证书中签名的公钥，获得 Bob 公钥

公钥证书主要内容

序列号：唯一发行号
证书持有者信息，包括算法和密钥值
证书发行者信息， CA 信息
有效期
发行者数字签名

KDC 解决对称密钥问题，CA 解决公钥问题。

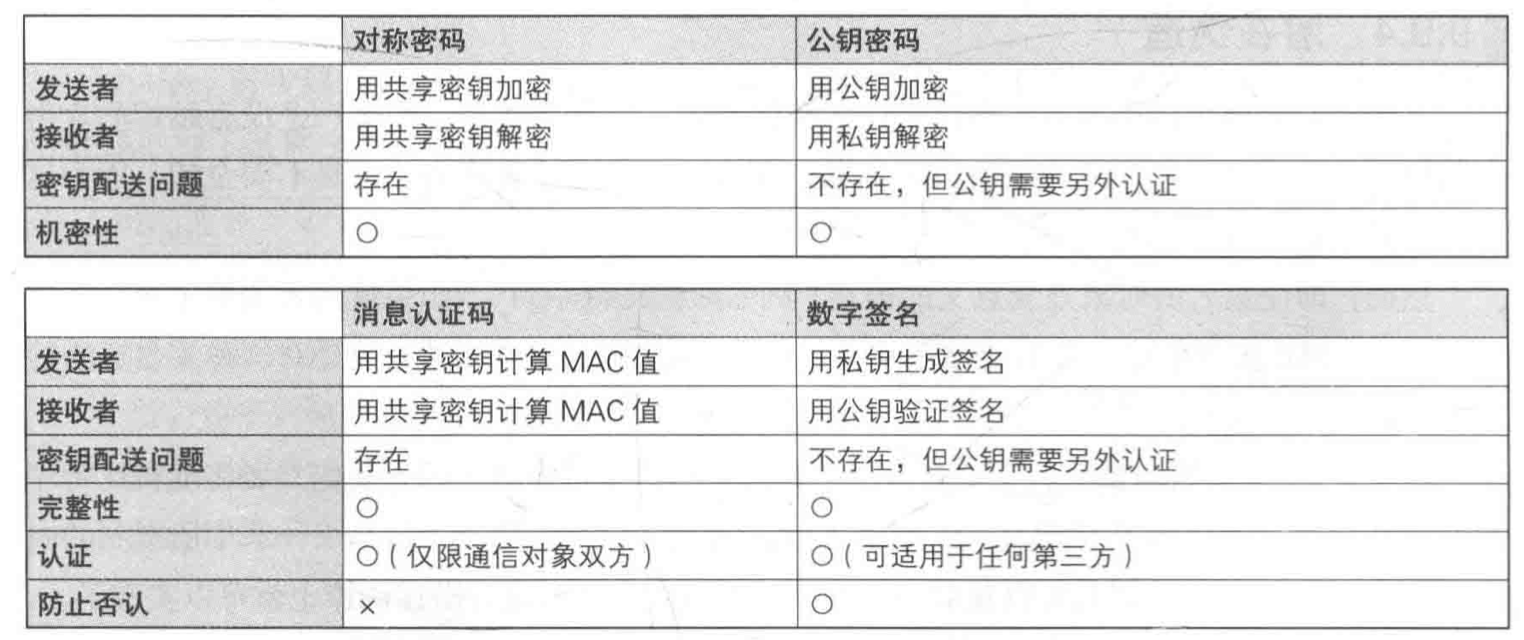
对称密码的密钥是机密性的精华 ，单向散列函数的散列值是完整性的精华。

为什么一般都是先压缩再加密？

这是因为在加密之后，比特序列的冗余性消失，基本上无法进行压缩了。在加密前进行压
缩的做法不仅限于混合密码系统，而是对所有密码都适用的。

PGP web of trust.

除了 CA 之外，还有其他的方式对公钥合法性进行认证，比如 PGP 的信任网络。